函式煉金
原文是透過 函式養殖 來比喻, 這邊用 煉金術 來比喻
下面是 compose
const compose =
(...fns) =>
(...args) =>
fns.reduceRight((res, fn) => [fn.call(null, ...res)], args)[0];
... 別害怕!這是戰鬥力突破 9000 的超級賽亞人版 compose。 先讓我們忘了這個版本的實作,來思考如何用簡單的形式將兩個函式結合在一起。 當你徹底理解之後,就可以將它抽象化,並可以簡單的將它應用在函式上不論數量多少。 (你甚至可以嘗試證明它!)
抽象化,也可以稱作概念化, 是指將某些事物或是情報統合成一個 概念 或是 詞彙, 主要是為了降低複雜度,用簡單的概念來控制或認識事物。 抽象化普遍存在於所有人類,也是證明你是人類的基本特徵。
那這邊給你比較和藹可親的版本,親愛的小讀者:
const compose2 = (f, g) => (x) => f(g(x));
f 和 g 都是函式,而 x 是個貫通他們的值。
函式結合就像是在做函式煉金術, 你就是煉金術師, 選擇兩個你想要的特徵,然後把他們合成組合在一起生成一個新的。 下面示範做法:
const toUpperCase = (x) => x.toUpperCase();
const exclaim = (x) => `${x}!`;
const shout = compose(exclaim, toUpperCase);
shout("send in the clowns"); // "SEND IN THE CLOWNS!"
兩個函式的結合回傳了一個新的函式。 這很符合邏輯:組合兩個同樣型態的東西 (這邊的例子是函式) 應該也要得到一個同樣型態的新東西。 把兩個樂高積木拼在一起並不會變成木質積木。 這是有理論在背後的,接下來我們會探討它背後的機制。
在我們制定的 compose 中,g 會比 f 先跑,會建立一個由右到左的資料流。
這遠比巢狀的函式調用可讀性更好,如果不使用的情況如下:
const shout = (x) => exclaim(toUpperCase(x));
比起從內到外,讓我們從右到左, 我們接著了解,為什麼順序很重要:
const head = (x) => x[0];
const reverse = reduce((acc, x) => [x, ...acc], []);
const last = compose(head, reverse);
last(["jumpkick", "roundhouse", "uppercut"]); // 'uppercut'
reverse 會將 list 反轉,而 head 取其第一個元素。
而這個結果就是得到了一個效能不高的 last 函式。
這些函式組合的順序應該顯而易見。
當然我們可以定義一個從左到右的版本,
但是,從右向左執行更加符合數學定義。
實際上,我們該來看一個所有組合都有的特性了。
// associativity 結合律
compose(f, compose(g, h)) === compose(compose(f, g), h);
這特性就是結合律,上面兩組不論你如何組合,都不會影響結果,如同上面。 所以,假設我們要把字串的首字母大寫,我們可以這樣寫:
compose(toUpperCase, compose(head, reverse));
// or
compose(compose(toUpperCase, head), reverse);
我們如何透過 compose 組合這些群組不太重要,因為結果都是一樣的。
這讓我們可以寫出更多變化的組合,就像接下來的示範:
// 我們之前需要寫兩個 compose,但因為結合律,
// 無論多少個函式我們都可以結合,讓我們自己決定如何配對他們
const arg = ["jumpkick", "roundhouse", "uppercut"];
const lastUpper = compose(toUpperCase, head, reverse);
const loudLastUpper = compose(exclaim, toUpperCase, head, reverse);
lastUpper(arg); // 'UPPERCUT'
loudLastUpper(arg); // 'UPPERCUT!'
透過結合律這個特性,我們同時獲得了彈性跟心靈平靜,因為其結果都會相等。 更加複雜的另一種寫法可以在本書中的附錄中找到, 這是更加普遍的版本,你可以在一些套件像是 lodash, underscore, ramda 中找到。
結合律另一個更香的特性就是,其中的任何組合都可以被另外抽出來組合。 我們來重構一下之前的例子:
const loudLastUpper = compose(exclaim, toUpperCase, head, reverse);
// -- or ---------------------------------------------------------------
const last = compose(head, reverse);
const loudLastUpper = compose(exclaim, toUpperCase, last);
// -- or ---------------------------------------------------------------
const last = compose(head, reverse);
const angry = compose(exclaim, toUpperCase);
const loudLastUpper = compose(angry, last);
// more variations...
這邊沒有絕對的對錯 - 我們只是按照自己的喜好拼裝樂高而已。
通常來說,最好是像 last 跟 angry 一樣可以自由的組合跟重複利用。
如果有看過 馬丁福勒的 "重構 Refactoring",
就會發現這個過程就是 抽離 extract function"...
但我們不再需要關心物件狀態。
Pointfree
Pointfree 指的就是函式不需要特別標註他要如何操作資料。 一級函式,科里化,還有結合都非常適合這種寫法風格。
小提示: Pointfree 版本的
replace和toLowerCase可以在 Appendix C - Pointfree Utilities 找到. 快去看看!
// not pointfree because we mention the data: word
const snakeCase = (word) => word.toLowerCase().replace(/\s+/gi, "_");
// pointfree
const snakeCase = compose(replace(/\s+/gi, "_"), toLowerCase);
看到我們是怎麼局部調用 replace 了嗎?
我們在這邊做的事情就是把我們的資料貫通每個函式。
科里化讓我們可以提前準備好每個函式,讓函式只需要接到資料,處理它,把他傳到下一步。
另外注意到,在 pointful 的版本中,我們必須透過 word 才能進行接下來的操作,
但是在 pointfree 的版本,我們不需要依賴資料構築我們的函式。
讓我們看看其他範例。
// not pointfree because we mention the data: name
const initials = (name) =>
name.split(" ").map(compose(toUpperCase, head)).join(". ");
// pointfree
// NOTE: we use 'intercalate' from the appendix instead of 'join' introduced in Chapter 09!
const initials = compose(
intercalate(". "),
map(compose(toUpperCase, head)),
split(" ")
);
initials("hunter stockton thompson"); // 'H. S. T'
Pointfree 的風格能夠幫助我們減少不必要的命名,讓程式碼保持簡潔跟通用。
它也是很好的檢驗方式,
讓我們看出某段程式碼是否符合函式編程,透過每個小函式是否可以透過 input 跟 output 傳接資料。
譬如,while 是不能組合的。
不過也需要特別警惕,pointfree 是把雙面刃,有時候他也會混淆意圖,
並非所有函式編程都需要 pointfree ,沒有也是無所謂的,
該用的時候就用,不能用的時候就用普通的執行方式。
Debugging
在使用結合的時候,比較會遇到的常見錯誤是,
在沒有做局部調用之前就組合類似像 map 這樣需要兩個參數的函式。
// 錯 - 最後根本不知道 `angry` 傳了什麼東西給 `map`
const latin = compose(map, angry, reverse);
latin(["frog", "eyes"]); // error
// 對 - 每個函式預計接受一個參數
const latin = compose(map(angry), reverse);
latin(["frog", "eyes"]); // ['EYES!', 'FROG!'])
如果你需要 debug 組合函式的話,
你可以使用好用但不純的 trace 函式來看看到底發生什麼事。
const trace = curry((tag, x) => {
console.log(tag, x);
return x;
});
const dasherize = compose(
intercalate("-"),
toLower,
split(" "),
replace(/\s{2,}/gi, " ")
);
dasherize("The world is a vampire");
// TypeError: Cannot read property 'apply' of undefined
這裡報錯了,我們來 trace 看看
const dasherize = compose(
intercalate("-"),
toLower,
trace("after split"),
split(" "),
replace(/\s{2,}/gi, " ")
);
dasherize("The world is a vampire");
// after split [ 'The', 'world', 'is', 'a', 'vampire' ]
喔!我們需要透過 map 來把陣列中的字串 toLower
const dasherize = compose(
intercalate("-"),
map(toLower),
split(" "),
replace(/\s{2,}/gi, " ")
);
dasherize("The world is a vampire"); // 'the-world-is-a-vampire'
除錯時,trace 函式允許我們在某個時間點觀測資料,
在 Haskell 或是 PureScript 這類的語言也有類似的函式以便於我們開發。
結合將會變成我們架構程式的工具, 而幸運的是,他背後是有強大的理論基礎在背後支撐的, 讓我們來研究下這套理論。
範疇論
範疇論是數學的其中一個抽象分支, 能夠統整像是集合論、類型論、群論,邏輯這些不同分支的概念。 主要針對像是 物件,態射和轉換式等,這些跟撰寫程式有非常緊密的關係。 這邊有張圖表標示同樣的概念在不同的理論中的形式。
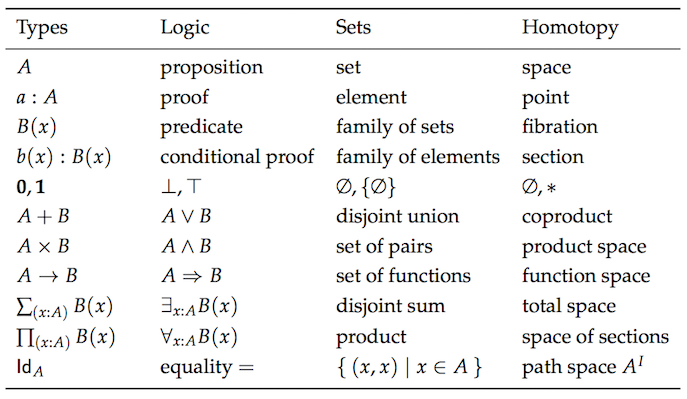
抱歉,我並沒有要嚇爛你的意思, 我並不預設你對這些概念都瞭如指掌。 我的用意是要讓你看看這邊有多少重複的內容, 讓你了解為什麼需要用範疇論統一這些概念。
在範疇論中,我們有個東西叫 ... 範疇。 透過了以下一些元件組合起來就構成範疇了。
- 物件的集合
- 態射的集合
- 態射的組合
- 其中 identity 是比較特別的態射
範疇論是抽象到足以模擬任何事物的, 但我們目前先關注型別跟函式就好了。
物件的集合
物件就是資料類型。例如,String, Boolean, Number, Object 等等。
我們通常將型別視為該資料所有可能的值的集合。
像是 Boolean 就是 [true, false] 的集合,Number 就是所有實數的集合。
把型別當作集合來思考的好處就是可以套用集合論。
態射的集合 態射就是標準的純函式
態射的組合
對,你可能已經猜到了,這就是我們這章的新玩具 - compose。
我們已經討論過 compose 函式是符合結合律的,
這並非是巧合,結合律是在範疇論中對任意組合皆適用的特性。
這邊的圖展示了什麼是組合:
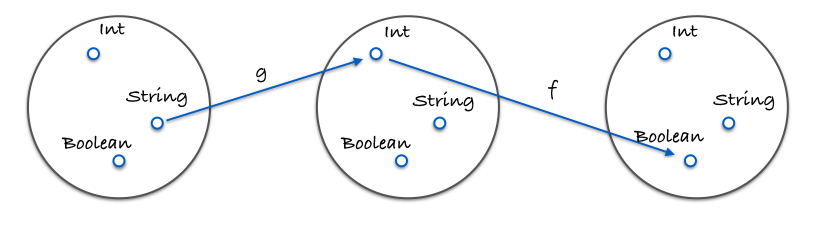
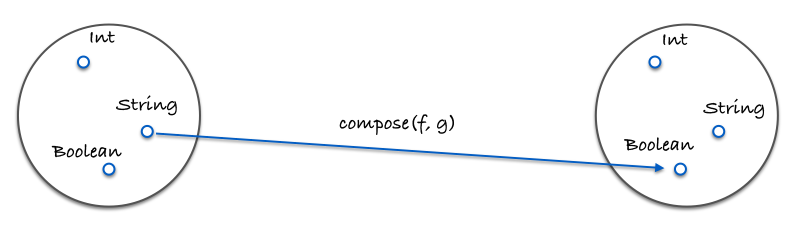
這邊是程式碼:
const g = (x) => x.length;
const f = (x) => x === 4;
const isFourLetterWord = compose(f, g);
其中 identity 是比較特別的態射
讓我們介紹一個很實用的函式 id,
這個函式就是把你傳進去的值原封不動地再傳出來給你:
const id = (x) => x;
你可能會問 "這到底有個X用?" 別急,我們會在後面的章節大量的使用到的, 但現在你可以暫時把它當作,一個把自己當作資料本身的函式。
id 跟組合的搭配簡直完美。
下面的特性永遠適用於任意一元函式 (只有一個參數的函式):
// identity
(compose(id, f) === compose(f, id)) === f;
// true
是不是很像是數字的單位元!
如果這還不夠清楚,可以多花點時間。
我們很快就會到處使用 id 了,
不過這邊暫時將它當作是替代數值的函式。
這對寫 pointfree 來說非常好用。
以上就是型別與函式的範疇論了。 如果這是你第一次聽到這些概念,我估計你應該還是有些聽無,不知道範疇論到底在幹嘛,有什麼用。 沒關係,本書全書都在借助這些知識。
至於現在,這個章節,從這行開始,
你至少可以認定它向我們提供了些有關於結合的知識 - 譬如 結合律 跟 單元率。
那還有其他的範疇嗎?
我們可以定義一個向量圖,以節點作為物件,邊作為態射,路徑作為組合。
還可以定義 實數 作為物件, >= 作為 態射 (實際上任何偏序或是全序都可以作為一個範疇)。
範疇是無限的,但以本書的宗旨來說,
我們只需要關心上面提到的內容即可。
至此我們已經初略的理解這些必要內容了。
總結
組合就像是接水管一樣將函式串聯在一起。 而資料將會在此貫穿我們的應用程式。 畢竟,純函式就是輸入對應到輸出而已, 所以當你打破了這個連結時就使得我們的軟體變得無用。
我們認為 結合 是最高設計原則, 就是因為 結合 讓我們的程式碼變得簡單且更有彈性。 另外 範疇論 在 應用程式架構,模擬副作用,確保正確性 扮演了很重要的角色。
現在我們已經具備了足夠的知識,接下來就讓我們來寫一些練習範例。
